3174. Северо – восточный король

В левом нижнем углу квадратной шахматной доски n × n находится король. Он может ходить только на одну клетку вправо, вверх, или по диагонали вправо вверх. Посчитайте количество способов, которыми король может дойти до правой верхней клетки доски по модулю 1000003.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 1000). Следующие t строк содержат по одному целому числу n (1 ≤ n ≤ 1000).

Выход. Для каждого значения n выведите в отдельной строке искомое количество способов.

Пример входа	Пример выхода
2 2 3	3 13

РЕШЕНИЕ

динамическое программирование

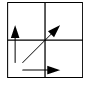
Анализ алгоритма

Из любой клетки король может передвигаться на одну клетку вправо, вверх, или по диагонали вправо вверх.

Пусть dp – двумерный массив, в котором dp[i][j] равно количеству способов, которыми король может добраться из (1, 1) в (i, j). Положим dp[1][1] = 1.

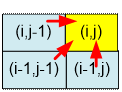
В клетку (i, j) король может попасть из (i – 1, j), из (i, j – 1) или из (i – 1, j – 1). Следовательно

dp[i][j] = dp[i – 1][j] + dp[i][j – 1] + dp[i – 1][j – 1]

Изначально обнулим массив dp. Для нас будет существенным обнуление нулевой строки и нулевого столбца массива dp. Если, например i = 1, то dp[i – 1][j] = dp[0][j] = 0 и тогда уравнение динамики превратится в dp[i][j] = dp[i][j – 1] (так пересчитывается первая строка). Если же j = 1, то уравнение динамики примет вид dp[i][j] = dp[i – 1][j] (так пересчитывается первый столбец). Учитывая что dp[1][1] = 1 можно заключить, что первый столбец и первая строка во всех ячейках будет содержать 1.

Пример

Заполним массив dp для поля размером 4 * 4:

Реализация алгоритма

Объявим рабочий массив dp.

#define MAX 1001

#define MOD 1000003

int dp[MAX][MAX];

Заполним ячейки массива dp.

memset(dp, 0, sizeof(dp));

dp[0][0] = 1;

for (i = 1; i < MAX; i++)

for (j = 1; j < MAX; j++)

dp[i][j] = (dp[i - 1][j] + dp[i][j - 1] + dp[i - 1][j - 1]) % MOD;

Читаем входные данные. Для каждого значения n выводим dp[n][n].

scanf("%d", &tests);

while (tests--)

{

scanf("%d", &n);

printf("%d\n", dp[n][n]);

}